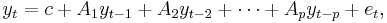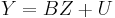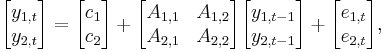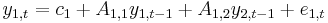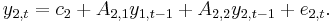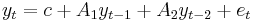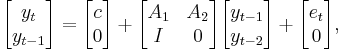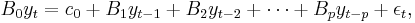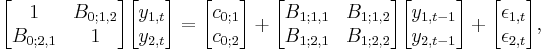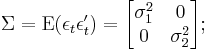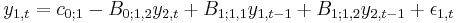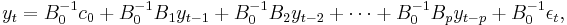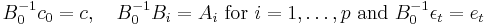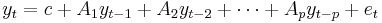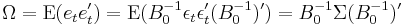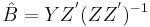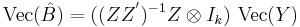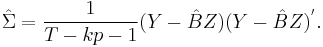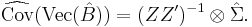Vector autoregression
Vector autoregression (VAR) is a statistical model used to capture the linear interdependencies among multiple time series. VAR models generalize the univariate autoregression (AR) models. All the variables in a VAR are treated symmetrically; each variable has an equation explaining its evolution based on its own lags and the lags of all the other variables in the model. VAR modeling does not require expert knowledge, which previously had been used in structural models with simultaneous equations.
VAR models were advocated by Christopher Sims, who criticized the claims and performance of earlier modeling in macroeconomic econometrics. Sims recommended VAR models, which had previously appeared in time series statistics and system identification, a statistical specialty in control theory. Sims advocated VAR models as providing a theory-free method to estimate economic relationships, thus being an alternative to the "incredible identification restrictions" in structural models.[1]. Sims was awarded the 2011 Nobel Prize in Economics for his work in applying VAR models to macroeconomic analysis.[2]
Contents |
Specification
Definition
A VAR model describes the evolution of a set of k variables (called endogenous variables) over the same sample period (t = 1, ..., T) as a linear function of only their past evolution. The variables are collected in a k × 1 vector yt, which has as the ith element yi,t the time t observation of variable yi. For example, if the ith variable is GDP, then yi,t is the value of GDP at t.
A (reduced) p-th order VAR, denoted VAR(p), is
where c is a k × 1 vector of constants (intercept), Ai is a k × k matrix (for every i = 1, ..., p) and et is a k × 1 vector of error terms satisfying
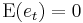 — every error term has mean zero;
— every error term has mean zero;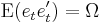 — the contemporaneous covariance matrix of error terms is Ω (a k × k positive-definite matrix);
— the contemporaneous covariance matrix of error terms is Ω (a k × k positive-definite matrix);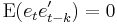 for any non-zero k — there is no correlation across time; in particular, no serial correlation in individual error terms.
for any non-zero k — there is no correlation across time; in particular, no serial correlation in individual error terms.
The l-periods back observation yt−l is called the l-th lag of y. Thus, a pth-order VAR is also called a VAR with p lags.
Order of integration of the variables
Note that all the variables used have to be of the same order of integration. We have so the following cases:
- All the variables are I(0) (stationary): one is in the standard case, i.e. a VAR in level
- All the variables are I(d) (non-stationary) with d>0:
- The variables are cointegrated: the error correction term has to be included in the VAR. The model becomes a Vector error correction model (VECM) which can be seen as a restricted VAR.
- The variables are not cointegrated: the variables have first to be differenced d times and one has a VAR in difference.
Concise matrix notation
One can write a VAR(p) with a concise matrix notation:
Details of the matrices are in a separate page.
Example
For a general example of a VAR(p) with k variables, please see this page.
A VAR(1) in two variables can be written in matrix form (more compact notation) as
or, equivalently, as the following system of two equations
Note that there is one equation for each variable in the model. Also note that the current (time t) observation of each variable depends on its own lags as well as on the lags of each other variable in the VAR.
Writing VAR(p) as VAR(1)
A VAR with p lags can always be equivalently rewritten as a VAR with only one lag by appropriately redefining the dependent variable. The transformation amounts to merely stacking the lags of the VAR(p) variable in the new VAR(1) dependent variable and appending identities to complete the number of equations.
For example, the VAR(2) model
can be recast as the VAR(1) model
where I is the identity matrix.
The equivalent VAR(1) form is more convenient for analytical derivations and allows more compact statements.
Structural vs. reduced form
Structural VAR
A structural VAR with p lags (sometimes abbreviated SVAR) is
where c0 is a k × 1 vector of constants, Bi is a k × k matrix (for every i = 0, ..., p) and εt is a k × 1 vector of error terms. The main diagonal terms of the B0 matrix (the coefficients on the ith variable in the ith equation) are scaled to 1.
The error terms εt (structural shocks) satisfy the conditions (1) - (3) in the definition above, with the particularity that all the elements off the main diagonal of the covariance matrix 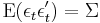 are zero. That is, the structural shocks are uncorrelated.
are zero. That is, the structural shocks are uncorrelated.
For example, a two variable structural VAR(1) is:
where
that is, the variances of the structural shocks are denoted 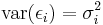 (i = 1, 2) and the covariance is
(i = 1, 2) and the covariance is 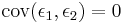 .
.
Writing the first equation explicitly and passing y2,t to the right hand side one obtains
Note that y2,t can have a contemporaneous effect on y1,t if B0;1,2 is not zero. This is different from the case when B0 is the identity matrix (all off-diagonal elements are zero — the case in the initial definition), when y2,t can impact directly y1,t+1 and subsequent future values, but not y1,t.
Because of the parameter identification problem, ordinary least squares estimation of the structural VAR would yield inconsistent parameter estimates. This problem can be overcome by rewriting the VAR in reduced form.
From an economic point of view it is considered that, if the joint dynamics of a set of variables can be represented by a VAR model, then the structural form is a depiction of the underlying, "structural", economic relationships. Two features of the structural form make it the preferred candidate to represent the underlying relations:
- 1. Error terms are not correlated. The structural, economic shocks which drive the dynamics of the economic variables are assumed to be independent, which implies zero correlation between error terms as a desired property. This is helpful for separating out the effects of economically unrelated influences in the VAR. For instance, there is no reason why an oil price shock (as an example of a supply shock) should be related to a shift in consumers' preferences towards a style of clothing (as an example of a demand shock); therefore one would expect these factors to be statistically independent.
- 2. Variables can have a contemporaneous impact on other variables. This is a desirable feature especially when using low frequency data. For example, an indirect tax rate increase would not affect tax revenues the day the decision is announced, but one could find an effect in that quarter's data.
Reduced-form VAR
By premultiplying the structural VAR with the inverse of B0
and denoting
one obtains the pth order reduced VAR
Note that in the reduced form all right hand side variables are predetermined at time t. As there are no time t endogenous variables on the right hand side, no variable has a direct contemporaneous effect on other variables in the model.
However, the error terms in the reduced VAR are composites of the structural shocks et = B0−1εt. Thus, the occurrence of one structural shock εi,t can potentially lead to the occurrence of shocks in all error terms ej,t, thus creating contemporaneous movement in all endogenous variables. Consequently, the covariance matrix of the reduced VAR
can have non-zero off-diagonal elements, thus allowing non-zero correlation between error terms.
Estimation
Estimation of the regression parameters
Starting from the concise matrix notation (for details see this annex):
- The Multivariate Least Square (MLS) for B yields:
It can be written alternatively as:
Where  denotes the Kronecker product and Vec the vectorization of the matrix Y.
denotes the Kronecker product and Vec the vectorization of the matrix Y.
This estimator is consistent and asymptotically efficient. It is furthermore equal to the conditional maximum likelihood estimator (MLE) (Hamilton 1994, p 293).
- As the explanatory variables are the same in each equation, the Multivariate Least Square is equivalent to the Ordinary least squares(OLS) estimator applied to each equation separately, as was shown by Zellner (1962).
Estimation of the covariance matrix of the errors
As in the standard case, the MLE estimator of the covariance matrix differs from the OLS estimator.
MLE estimator: 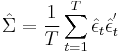
OLS estimator: 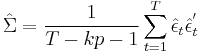 for a model with a constant, k variables and p lags
for a model with a constant, k variables and p lags
In a matrix notation, this gives:
Estimation of the estimator's covariance matrix
The covariance matrix of the parameters can be estimated as
Software
- R: there is a package vars which deals with VAR models[3].
- SAS: VARMAX
- STATA: "var"
- EViews: "VAR"
- Gretl: "var"
- RATS
- [ARFit]:
- [1] Time Series Analysis toolbox for Octave and Matlab: MVAR
See also
References
- Walter Enders, Applied Econometric Time Series, 2nd Edition, John Wiley & Sons 2003, ISBN 0-471-23065-0
- James D. Hamilton. Time Series Analysis. Princeton University Press. 1995.
- Helmut Lütkepohl. New Introduction to Multiple Time Series Analysis. Springer. 2005.
- Sims, Christopher (January 1980) [1977 (Working paper)], "Macroeconomics and reality" (pdf), Econometrica 48 (1): 1–48, JSTOR 1912017, http://www.econ.umn.edu/library/mnpapers/1977-91.pdf
- Arnold Zellner (1962) An Efficient Method of Estimating Seemingly Unrelated Regressions and Tests for Aggregation Bias. Journal of the American Statistical Association, Vol. 57, No. 298 (Jun., 1962), pp. 348–368.
Notes
- ^ Sims, Christopher (January 1980) [1977 (Working paper)], "Macroeconomics and reality" (pdf), Econometrica 48 (1): 1–48, JSTOR 1912017, http://www.econ.umn.edu/library/mnpapers/1977-91.pdf
- ^ Nobel press release, 2011.
- ^ Bernhard Pfaff VAR, SVAR and SVEC Models: Implementation Within R Package vars
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||